Class 10 RS Aggarwal Chapter 1 Real Number Solutions

Chapter 1 of RS Aggarwal for Class 10, “Real Numbers,” is all about understanding numbers and their basic properties. It covers important topics like finding HCF and LCM, using Euclid’s Division Lemma, and the Fundamental Theorem of Arithmetic. These concepts are simple and useful, helping students solve math problems easily. This chapter is a great way to build a strong base in mathematics and do well in exams.

In this blog, we will provide you with the Class 10 RS Aggarwal Solutions for Real Number. You can also download the PDF for easy access.

Class 10 RS Aggarwal Chapter 1 Real Number Solutions

The solutions provided here are designed to guide you step by step, making it easier to grasp each concept thoroughly

Q.1. What do you mean by Euclid’s division lemma?

Solution: For any two given positive integers a and b there exist unique whole numbers q and r such that

a = bq + r, when 0 ≤ r < b. 
Here, we call ‘a’ as dividend, b as divisor, q as quotient and r as remainder.
Dividend = (Divisor × Quotient) + Remainder

Q.2. A number when divided by 61 gives 27 as quotient and 32 as remainder. Find the number.
Solution: Using Euclid’s divison Lemma
Dividend = (Divisor × Quotient) + Remainder
= (61 × 27) + 32
= 1647 + 32
= 1679
Required number = 1679

Q.3. By what number should 1365 be divided to get 31 as quotient and 32 as remainder?
Solution: By Euclid’s Division Algorithm, we have:
Dividend = (Divisor × Quotient) + Remainder
1365 = (Divisor × 31) + 32
(1365 – 32) / 31 = Divisor
⇒ 1333 / 31 = Divisor
Therefore, Divisor = 43

Q.4. Using Euclid’s algorithm, find the HCF of:
(i) 405 and 2520
(ii) 504 and 1188
(iii) 960 and 1575
Solution:
(i) On dividing 2520 by 405, we get
Quotient = 6, remainder = 90
Therefore, 2520 = (405 × 6) + 90

Dividing 405 by 90, we get

Quotient = 4,

Remainder = 45

Therefore, 405 = 90 × 4 + 45
Dividing 90 by 45

Quotient = 2, remainder = 0
Therefore, 90 = 45 × 2
H.C.F. of 405 and 2520 is 45

(ii) Dividing 1188 by 504, we get

Quotient = 2, remainder = 180
Therefore, 1188 = 504 × 2 + 180

Dividing 504 by 180

Quotient = 2, remainder = 144

Therefore, 504 = 180 × 2 + 144

Dividing 180 by 144, we get

Quotient = 1, remainder = 36

Dividing 144 by 36

Quotient = 4, remainder = 0

Therefore, H.C.F. of 1188 and 504 is 36

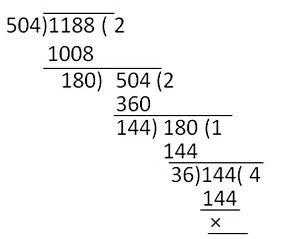
(iii) Dividing 1575 by 960, we get
Quotient = 1, remainder = 615
1575 = 960 x 1 + 615
Dividing 960 by 615, we get Quotient = 1, remainder = 345
960 = 615 x 1 + 345
Dividing 615 by 345 Quotient = 1, remainder = 270
615 = 345 x 1 + 270
Dividing 345 by 270, we get Quotient = 1, remainder = 75
345 = 270 x 1 + 75
Dividing 270 by 75, we get Quotient = 3, remainder =45
270 = 75 x 3 + 45
Dividing 75 by 45, we get Quotient = 1, remainder = 30
75 = 45 x 1 + 30
Dividing 45 by 30, we get Remainder = 15, quotient = 1
45 = 30 x 1 + 15
Dividing 30 by 15, we get Quotient = 2, remainder = 0
H.C.F. of 1575 and 960 is 15

Q.5. Show that every positive integer is either even or odd.
Solution: Let a be a given positive integer.
On dividing a by 2, let q be the quotient and r be the remainder.
Then, by Eudid’s algorithm, we have
a = 2q+ r, where 0 < r < 2
⇒ a = 2q + r, where r = 0,1
⇒ a = 2q or a = 2q + 1
When a = 2q for some integer q, then clearly a is even.

When a = 2q + 1 for some integer q, then dearly a is odd.

Thus, every positive integer is either even or odd.

Q.6. Show that any positive odd integer is of the form (6m + 1) or (6m + 3) or (6m + 5), where m is some integer.
Solution: Let a be a given positive integer.
On dividing a by 6, let q be the quotient and r be the remainder.
Then, by Eudid’s algorithm, we have
a = 6q + r, where 0 < r < 6
⇒ a = 6q + r, where r = 0,1,2,3,4,5,6
⇒ a = 6q or a = 6q + 1 or a = 6q + 2 or a = 6q + 3 or a = 6q + 4 or a = 6q + 5
But, a = 6q, a = 6q + 2, a = 6q + 4 gives even values of a.
Thus, when a is odd, it is of the form
6q + 1, 6q + 3 or 6q + 5 for some integer q.

Q.7. Show that any positive odd integer is of the form (4m + 1) or (4m + 3), where in is some integer.
Solution: 
Let a be a given positive odd integer.
On dividing aby 4, let qbe the quotient andr be theremainder.
Then, by Eudid’s algorithm, we have
a = 4m + r, where 0 < r < 4
⇒ a = 4m + r, where r = 0,1,2,3
⇒ a = 4m or a = 4m + 1 or a = 4m + 2 or a = 4m + 3
But, a = 4m and a = 4m + 2 = 2(2m + 1) are clearly even.
Thus, when ais odd, it is of the form a = (4m + 1)or (4m + 3) for some integer m.